
Energy efficient museum storageCopenhagen, 10 - 11 October 2013 Calculation tools and basic concepts Lectures (too many!) Cambridge, 15 October 2013 Paris-CRCC |
Glossary of the microclimate variables and units used in conservation physicsTemperatureTemperature is a measure of the kinetic energy of moving molecules. Moving molecules of a gas exert a pressure on their container when they bounce off it, which can be used to define a temperature scale. The temperature in degrees kelvin (K) is the pressure in pascal of one mole of gas in a container of one cubic metre, divided by 8.31 (the gas constant). This definition requires some sub-definitions to clarify it: The unit of pressure pascal (Pa) is 1 newton per square metre. It is worth noting that atmospheric pressure is about 100,000 Pa. The newton (N) is the force which will accelerate a mass of 1 kg by 1 m/s2. That is approximately the force exerted downward on your hand when you are holding 100 g of something. The mole is the standard amount of any substance, usually expressed as the weight of a particular number of its molecules. Formally, it is the amount of any substance which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12. You get to choose what is an entity: an atom, a molecule or something else. Finally, the gas constant R is invoked to reconcile the various units. One mole, or mol, of water weighs 18 g. Basically, temperature is a measure of the physical turmoil within materials. In a gas at room temperature the molecules are buzzing about at around 400 km/s. The non-fundamental but universally used (except in the USA) celsius (°C) scale is degrees kelvin minus 273.15, which has a value close to zero for melting ice and a value of 100 for boiling water at sea level. Note that there is a tradition in physics to quote temperature differences in degrees K rather than C, though the number is the same. Temperature measurement. It is not easy to measure the pressure of a gas in a hand-held instrument, so many indirect methods are in use, some of which also use expansion with increasing molecular movement: the mercury or alcohol thermometer for example. Other methods use changes in subtler effects of atomic vibration: electrical resistance thermometers and thermocouples. In conservation, temperature is important because increasing molecular vibration is believed to be the cause of the exponentially increasing reaction rate of decay processes, according to theories of chemical kinetics, which are explained elsewhere in this series of articles. Temperature change also causes phase changes in materials, as atoms re-arrange their relative positions to accommodate more vibration at higher temperature. The varying expansion with temperature of different materials causes shear stresses to develop in laminated objects such as paintings, veneered furniture and film. HeatHeat is the form of energy that moves between two bodies at different temperatures when they are brought into contact. Two materials put in contact will even out the kinetic energy of their particles by transferring vibration over the interface. It is this transfer of kinetic energy which is defined as heat. Heat should not be confused with temperature. Temperature is a potential - two bodies of the same composition but of different size can have the same temperature but when the smaller body is brought into contact with a third body, less heat will be transferred than if the larger body was brought into contact. We call heat an extensive property - it depends on the amount of substance, whereas temperature is a potential which does not depend on the amount of substance, only on the average kinetic energy of its particles, however few they may be. The unit of heat is the joule (J), which has the dimension newton x metre. That is the kinetic energy of a 1 kg object moving at 1 m/s. Heat is just one form of energy: there are other forms of energy held within a mass of material, such as chemical bonding energy, as mentioned above in connection with phase change materials. This is a cause of confusion because air conditioning engineers refer to the energy used in phase change as latent heat. They are usually referring to the energy used to vaporise water into an air space, to raise the relative humidity without causing any change of temperature. Heat is strictly speaking only that energy which is transferred across a temperature difference but it is here extended to include energy expended in forcing a phase change from liquid to gas. Heat capacityIf one brings together a hot and a cold body of equal size, the final uniform temperature will not generally be midway between the original temperatures. The size of the bodies matters but also their composition and density. So we must introduce another important concept: the heat capacity (Cp). This is the amount of energy needed to raise the temperature of unit mass of the material by one degree. The unit of mass varies among published values but is generally one gram, 1 kg or one mole. In the building physics community the unit is generally joules per kilogram. The subscript 'p' describes the heat capacity measured at constant pressure, which is nearly always what we intend, in everyday physics. The alternative is heat capacity measured at constant volume, with subscript 'v'. Radiative heat transferHeat is explained above as energy transferred by contact between two bodies. This is more precisely defined as conductive heat transfer, or convective heat transfer when moving air or liquid is involved. Heat can also be transferred by radiation through space, with no physical contact between the hotter and the cooler body. The agent of energy transfer is the electromagnetic disturbance of the surface molecules by the radiation, or the absorption of photon energy with subsequent transformation into vibration. The alternative visualisations are invoked according to the phenomenon being studied. The energy transferred through radiation is proportional to the fourth power of the kelvin temperature. Materials are not necessarily perfect emitters and absorbers of radiant energy, so the energy emitted must be multiplied by a factor between zero and one, called the emissivity coefficient. This coefficient varies with the wavelength (or photon energy) of the radiation. White marble, for example, reflects 0.7 of all the solar radiation. Its long wavelength, low temperature emissivity is 0.95, so it accepts only 30% of incoming solar radiation, which warms it up during the day, but efficiently re-radiates its accumulated heat energy to the night sky. This process makes a marble-clad building cooler, on average, than a building covered with a solar absorber, such as matt black paint, even though the paint will probably emit long wavelength radiation at night just as efficiently as marble. The variation of emissivity with wavelength is of considerable importance in designing low energy buildings. Atmospheric moistureAtmospheric water vapour is mixed with the other gases that constitute air. Water does not dissolve in air and does not interact in any way with molecules in air. This independence of atmospheric gases was established by John Dalton in 1801 as the law of partial pressures. Let us first consider the properties of water without any air present. In this special case the partial pressure of water vapour is also the total gas pressure. Imagine a stiff walled container with a pool of water in the bottom. Water will evaporate into the space up to a certain concentration. This is the concentration at which the rate of return of water molecules to the liquid surface, as a consequence of their random motion, equals the rate of escape into the vapour phase resulting from molecular collisions in the liquid water. The rate of escape increases exponentially with increasing temperature, but the rate of return is nearer proportional to the concentration in the vapour phase and the absolute temperature. The net result is increasing vapour concentration, and therefore increasing gas pressure, with rising temperature. The vapour pressure is shown in the graph below.  The vapour pressure diagram for water. The right y-axis shows the equivalent concentration. Finer lines trace the relative humidity. The top curve is the equilibrium pressure over a pure water surface. It is commonly called the saturation vapour pressure. In everyday life, even in the writer's damp home region, Devon UK, there is not usually this much water vapour around. The actual water vapour amount is commonly defined by the relative humidity (RH). This is the actual water vapour concentration expressed as a fraction of the saturation value at the same temperature. It is a pure number, so the unit of concentration, or vapour pressure, doesn't matter. Although RH is not a true concentration, it does accurately reflect the ability of the water vapour to do watery things, like absorbing into paper, participating in hydrolysis reactions and supporting mould growth. Biologists and chemists call the RH the water activity and express it as a fraction. Conservators and meteorologists generally use the term relative humidity and express it as a percentage, thus avoiding writing a decimal point and reflecting the difficulty of measuring the RH with better than one percent accuracy. The vapour pressure graph above is superficially similar to, but fundamentally different from, the psychrometric chart used by building engineers, and by conservators influenced by the classic book The museum environment by Garry Thomson. I think the vapour pressure diagram is simpler to use for most conservation purposes. The psychrometric chart, also called the Mollier diagram, first becomes useful when studying the subtleties of energy consumption in air conditioning systems. Returning to our imaginary airless container with a pool of water: if we now let air into this container there will be no change in the water vapour concentration. The water vapour concentration, and the partial water vapour pressure, are totally unaffected by the presence of air. Air is often used as a transporter of water vapour, especially in air conditioning ducts, which is why the engineers' psychrometric diagram uses the unit of kg of water per kg of air. This is convenient, but confusing. Usually, the careless description 'RH of air' does no harm, but it matters when considering the transport of art through the stratosphere. In spite of the dominance of relative humidity in our discourse, the water vapour concentration in kg/m3, or in kg/kg is a significant variable, because if a flow of outside air with a given RH and temperature moves into a room at a lower temperature, the water vapour concentration will not change much (just a little, because air contracts at a lower temperature) but the RH will rise considerably, as a study of the vapour pressure diagram will make clear. Therefore, when analysing the performance of a building standing in the natural climate, you will often be translating outside RH and temperature to concentration and then reversing the calculation to obtain the indoor RH value. Dew pointThere is a third way of defining the amount of water vapour in air. If air at 20°C and 50% RH is cooled to 10°C its position on the diagram will shift to the left nearly horizontally (because the vapour pressure hardly changes) to meet the saturation curve. This point is represented in the real world by dew on the surfaces or fog in the air. The dew point is a fictional temperature at which a space which is currently warm and dew free would reach condensation. Dew point is important in air conditioning, because conventional dehumidification relies on cooling air below the dew point to condense out water vapour, after which the air is re-heated and injected into the room. The dew point also limits the performance of air conditioning - it is a complicated matter to keep a room below 10°C and 50% RH because the dew point is then zero, so ice will form on the condensation dehumidifier, forcing the use of a different technology. The dew point also limits the performance of museum buildings: a museum held at 20°C and 50% RH will suffer condensation on single pane windows, or within the outer wall, when the outside temperature drops below 10°C. All these various ways of expressing the water content of air can be read from the vapour pressure diagram, except for the concentration in kg/kg, which depends on atmospheric pressure. Material response to temperature and relative humidityThe response of materials to changing temperature is described by their coefficient of thermal expansion, expressed in fractional change of dimension per degree. Many materials are anisotropic, expanding unequally in different directions. An important example in buildings is marble, whose calcite crystals expand unequally causing fragmentation of the structure of interlocking crystals. Thin marble veneers are prone to distortion. Generally, laminated materials develop shear stresses between and even within the layers as the temperature changes. The response of materials to changing RH is more complicated still. The general shape of the response is described as a sigmoid curve. The sorption curve for pure cellulose is shown here. 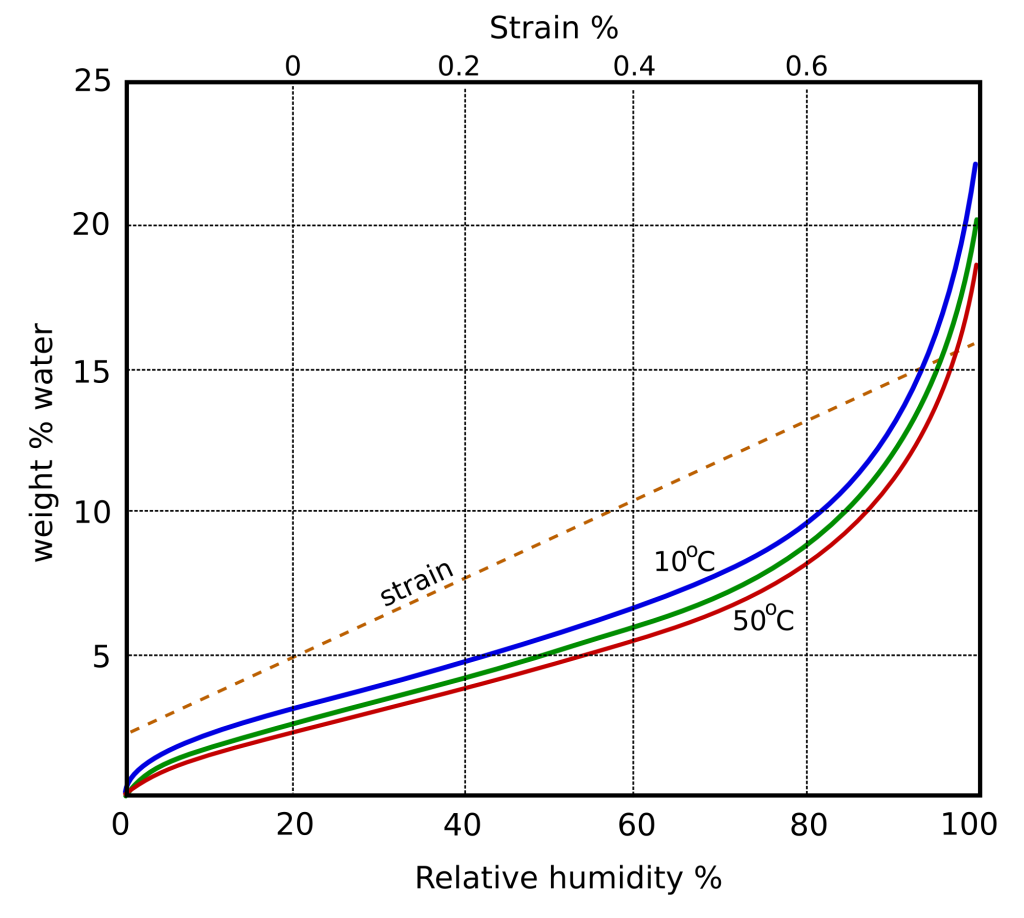 Note that the curve hardly moves over a large temperature change. In strong contrast to water in space (or air!), temperature change has little effect on the water content of cellulose at equilibrium with a fixed RH. The diagram is simplified because the curve is distinctly different depending on whether the curve is plotted with increasing or decreasing RH. This is known as hysteresis, and hardly matters in practice, though some conservators will disagree. The dotted line shows the dimensional change in paper caused by water absorption in the material. To read this value, choose a particular point on the sorption curve, then trace back horizontally to the strain line, then vertically to the scale at the top of the graph. Dimensional change in cellulosic materials consequent on RH change is larger, in the everyday variability of the weather, than dimensional change caused by temperature. Diffusion processesThe thermal conductivity (λ or k) is the proportionality constant in the Fourier equation which defines the heat flow through a material as proportional to the temperature gradient across it, in degrees per meter. The unit is usually watts per meter per degree. The watt is a joule per second. The thermal conductivity is a property of a single material, so it is not immediately useful in calculating heat loss through a wall. For this purpose it is more convenient to consider the temperature difference across the material, regardless of its thickness. The U value expresses the heat flux per square meter per degree temperature difference across the specimen. The temperature gradient is not explicitly defined, since it may vary through a laminated structure. The unit is watts per square meter per degree. The resistance to heat flow, the R-value is the reciprocal of the U value. Its usefulness is that it is additive: if you add insulation to an existing wall, just add the individual R values to get the total resistance. The thermal diffusivity is the ratio of the thermal conductivity to the heat capacity. This is an important concept. A material with a high heat capacity will impede transient heat flow, even if it has a high thermal conductivity. Since the natural temperature is not constant, the diffusivity is an important element in low energy design. Moisture diffusion through materialsAn analogous set of definitions describe moisture diffusion. Indeed, physicists describe water vapour diffusion by simply changing the name of the diffusion law from Fourier to Fick. Chemists will disagree with this as a greatly simplified analogy, but that is how all the predictive computer programs calculate water vapour diffusion. Vapour permeability (δ) is the ratio of moisture flux and the magnitude of the vapour pressure gradient. Its unit is kilograms per meter per pascal per second. It is an exact analog of thermal conductivity. Moisture diffusivity (Dw) is the ratio between the permeability and the moisture capacity, which is the gradient of the sorption curve displayed above. The unit is square meters per second. This also is analogous to the thermal diffusivity. Unfortunately, there is a rival definition of moisture diffusivity in the literature. The published descriptions of moisture movement through porous materials use a number of definitions, making the literature difficult to follow. A helpful reference is: M. Kumar Kumaran, International Energy Agency Annex 24 - Heat, air and moisture transfer through new and retrofitted insulated envelope parts (Hamtie). Final report, volume 3, Task 3: Material Properties. Published by Laboratorium Bouwfysica, K.U.-Leuven Belgium. 1996 ISBN 90-75741-01-4. With a title like this, one would think the book deserves oblivion, but it is actually a useful reference work. Otherwise wikipedia provides definitions of varying clarity. |