 |
Fundamental microclimate concepts |
Temperature is a measure of the kinetic energy of moving molecules. Moving molecules of a gas exert a pressure on their container when they bounce off it, which can be used to define a temperature scale. The temperature in degrees kelvin (K) is the pressure in pascal of one mole of gas in a container of one cubic metre, divided by 8.31 (the gas constant).
This definition requires some sub-definitions to clarify it: The unit of pressure pascal (Pa) is 1 newton per square metre. It is worth noting that atmospheric pressure is about 100,000 Pa. The newton (N) is the force which will accelerate a mass of 1 kg by 1 m/s2. That is approximately the force exerted downward on your hand when you are holding 100 g of something. The mole is the standard amount of any substance, usually expressed as the weight of a particular number of its molecules. Formally, it is the amount of any substance which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12. You get to choose what is an entity: an atom, an ion, a molecule or something else. Finally, the gas constant R is invoked to reconcile the various units. One mole, or mol, of water weighs 18 g.
Basically, temperature is a measure of the physical turmoil within materials. In a gas at room temperature the molecules are buzzing about at around 400 m/s. The non-fundamental but universally used (except in the USA) celsius (°C) scale is degrees kelvin minus 273.15, which has a value close to zero for melting ice and a value of 100 for boiling water at sea level. Note that there is a tradition in physics to quote temperature differences in degrees K rather than C, though the number is the same.
It is not easy to measure the pressure of a gas in a hand-held instrument, so many indirect methods are in use, some of which also use expansion with increasing molecular movement: the mercury or alcohol thermometer for example. Other methods use changes in subtler effects of atomic vibration: electrical resistance thermometers and thermocouples. The radiation intensity from a surface is an approximate measure of its temperature, as explained later.
In conservation, temperature is important because increasing molecular vibration is believed to be the cause of the exponentially increasing reaction rate of decay processes, according to theories of chemical kinetics, which are explained elsewhere in this series of articles. Temperature change also causes phase changes in materials, as atoms re-arrange their relative positions to accommodate more vibration at higher temperature. The varying expansion with temperature of different materials causes shear stresses to develop in laminated objects such as paintings, veneered furniture and film.
Heat is the form of energy that moves between two bodies at different temperatures when they are brought into contact. Two materials put in contact will even out the kinetic energy of their particles by transferring vibration over the interface. It is this transfer of kinetic energy which is defined as heat. We call heat an extensive property - it increases with the amount of substance at constant temperature, whereas temperature is a potential which does not depend on the amount of substance, only on the average kinetic energy of its particles, however few they may be. The unit of heat is the joule (J), which has the dimension newton x metre. That is the kinetic energy of a 1 kg object moving at 1 m/s.
Heat is just one form of energy. There are other forms of energy held within a mass of material, such as chemical bonding energy, as mentioned above in connection with phase change materials. This is a cause of confusion because air conditioning engineers refer to the energy used in phase change as latent heat. They are usually referring to the energy used to vaporise water into an air space, to raise the relative humidity without causing any change of temperature. Heat is strictly speaking only that energy which is transferred across a temperature difference, but it is here extended to include energy expended in forcing a phase change from liquid to gas, at constant temperature.
If one brings together a hot and a cold body of equal size but different composition, the final uniform temperature will not generally be midway between the original temperatures. So we must introduce another important concept: the heat capacity (Cp). This is the amount of energy needed to raise the temperature of unit mass of the material by one degree. The unit of mass varies among published values but is generally one gram, 1 kg or one mole. In the building physics community the unit is generally joules per kilogram. The subscript 'p' indicates the heat capacity measured at constant pressure, which is nearly always what we intend, in everyday life. The alternative is heat capacity measured at constant volume, with subscript 'v'.
Heat is explained above as energy transferred by contact between two bodies. This is more precisely defined as conductive heat transfer, or convective heat transfer when moving air or liquid is involved. Heat can also be transferred by radiation through space, with no physical contact between the hotter and the cooler body. The agent of energy transfer is the electromagnetic disturbance of the surface molecules by the radiation stream, or the absorption of photon energy with subsequent transformation into molecular vibration. One or other of these alternative visualisations is invoked according to the phenomenon being studied.
The energy transferred through radiation is proportional to the fourth power of the kelvin temperature. Materials are not necessarily perfect emitters and absorbers of radiant energy, so the energy emitted must be multiplied by a factor between zero and one, called the emissivity coefficient. This coefficient varies with the wavelength (or photon energy) of the radiation. White marble, for example, reflects 0.7 of all the solar radiation. Its long wavelength, low temperature emissivity is 0.95. Marble absorbs only 30% of incoming solar radiation, which warms it up a bit during the day, but it efficiently re-radiates its accumulated heat energy to the night sky. This process makes a marble-clad building cooler, on average, than a building covered with a good solar absorber, such as matt black paint. Even though the paint will emit long wavelength radiation at night just as efficiently as marble it absorbs much more solar radiation. The variation of emissivity with wavelength is of considerable importance in designing low energy buildings. Different pigments of almost the same colour have such different absorption in the infra red that they can influence the indoor temperature significantly.
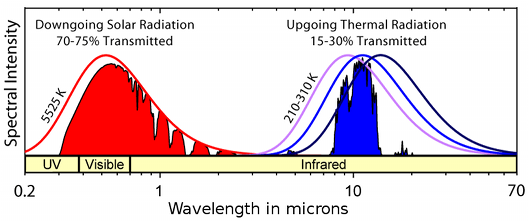
The atmosphere is transparent to much of the solar spectrum (red shading) but also to a band of long wavelength infra red radiation characteristic of emitters at terrestrial temperature (blue shading). The smooth curves are the black body radiation spectra for the sun and for the range of terrestrial temperatures.
Light energy is treated in more detail later in this glossary.
Atmospheric water vapour is mixed with the other gases that constitute air. Water does not dissolve in air and does not interact in any way with molecules in air. This independence of atmospheric gases was established by John Dalton in 1801 as the law of partial pressures.
Let us first consider the properties of water without any air present. In this special case the partial vapour pressure of water vapour is also the total gas pressure. Imagine a stiff walled container with a pool of water in the bottom. Water will evaporate into the space up to a certain concentration. This is the concentration at which the rate of return of water molecules to the liquid surface, as a consequence of their random motion, equals the rate of ejection into the vapour phase resulting from molecular collisions in the liquid water. The rate of escape increases exponentially with increasing temperature, but the rate of return is nearer proportional to the concentration in the vapour phase and to the absolute temperature. The net result is increasing vapour concentration, and therefore increasing gas pressure, with rising temperature. The vapour pressure is shown in the graph below.

The vapour pressure of water (highest curve). The right y-axis shows the equivalent concentration. The finer lines join points of constant relative humidity. Click on the image to display a high resolution version
The top curve is the equilibrium pressure over a pure water surface. It is commonly called the saturation vapour pressure. In everyday life there is not usually this much water vapour around. The water vapour concentration is commonly defined by the relative humidity (RH). This is the actual water vapour concentration expressed as a fraction of the saturation value at the same temperature. It is a ratio, so it doesn't matter which unit of concentration one chooses to use. Although RH does not define the concentration unless the temperature also is specified, it does accurately reflect the ability of the water vapour to do watery things, like absorbing into paper, participating in hydrolysis reactions and supporting mould growth. Biologists and chemists call the RH the water activity and express it as a fraction. Conservators and meteorologists generally use the term relative humidity and express it as a percentage, thus avoiding writing a decimal point and reflecting the difficulty of measuring the RH with better than one percent accuracy.
The vapour pressure graph is superficially similar to, but fundamentally different from, the psychrometric chart used by building engineers, and by conservators influenced by the classic book The museum environment by Garry Thomson. I think the vapour pressure diagram is simpler to use for most conservation purposes. The psychrometric chart, also called the Mollier diagram outside the Anglo-Saxon community, first becomes useful when studying the subtleties of energy consumption in air conditioning systems.
Returning to our imaginary airless container with a pool of water: if we now let air into this container there will be no change in the water vapour concentration. The water vapour concentration, and the partial water vapour pressure, are totally unaffected by the presence of air. Air is often used as a transporter of water vapour, especially in air conditioning ducts, which is why the engineers' psychrometric diagram uses the unit of kg of water per kg of air, so that separate diagrams are needed for each range of atmospheric pressure. Usually, the careless description 'RH of air' does no harm, but it matters when considering the transport of art through the stratosphere.
In spite of the deserved dominance of relative humidity in preventive conservation discussion, the water vapour concentration in kg/m3, or in kg/kg, is a significant variable, because if a flow of outside air with a given RH and temperature moves into a room at a lower temperature, the water vapour concentration will not change much (just a little, because gases contract at a lower temperature) but the RH will rise considerably, as a study of the vapour pressure diagram will make clear: as you move your finger horizontally to the left on the diagram, signifying lowering the temperature of a volume with constant water vapour content, you pass through lines of rising RH.
Therefore, when analysing the performance of a building standing in the natural climate, you will often be translating outside RH and temperature to concentration and then reversing the calculation to obtain the indoor RH.
There is yet another way of defining the amount of water vapour in air. If air at 20°C and 50% RH is cooled to 10°C its position on the diagram will shift to the left nearly horizontally (because the vapour pressure hardly changes) to meet the saturation curve. This point is represented in the real world by dew on surfaces or fog in the air. The dew point is a fictional temperature at which a space which is currently warm and dew free would reach condensation. Dew point is important in air conditioning, because conventional dehumidification relies on cooling air below the dew point to condense out water vapour, after which the air is re-heated and injected into the room. The dew point also limits the performance of air conditioning - it is a complicated matter to keep a room below 10°C and 50% RH because the dew point is then zero, so ice will form on the condensation dehumidifier, forcing the use of a different technology. The dew point also limits the performance of museum buildings: a museum held at 20°C and 50% RH will suffer condensation on single pane windows, or within the outer wall, when the outside temperature drops below 10°C.
All these various ways of expressing the water content of air can be read from the vapour pressure diagram, except for the concentration in kg/kg, which depends on atmospheric pressure.
Hygroscopic materials change weight, length, electrical resistance, electrical capacitance, and other properties as they absorb water, so diverse materials are used as humidity sensors which require calibration. The dew point sensor uses calibrated temperature sensors to measure the ambient temperature and also the temperature of a cooled mirror at the exact point at which it clouds over with dew. The psychrometer measures the ambient temperature and the lower temperature of a material evaporating water into an air stream. If you believe the temperature calibration, both the dew point sensor and the psychrometer can be regarded as fundamental devices both for measuring RH and for calibrating the more convenient sensors based on change of material properties.
The response of materials to changing temperature is described by their coefficient of thermal expansion, expressed in fractional change of dimension per degree. Some materials are anisotropic, expanding unequally in different directions. An important example in buildings is marble, whose calcite crystals expand unequally, causing fragmentation of the structure of interlocking crystals. Thin marble veneers are prone to distortion. Generally, laminated materials develop shear stresses between and even within the layers as the temperature changes.
The response of materials to changing RH is more complicated. The general shape of the response of water absorbent materials is described as a sigmoid curve. The sorption curve for pure cellulose is shown here.
Note that the curve hardly moves over a large temperature change. In strong contrast to water vapour in space, temperature change has little effect on the water content of cellulose at equilibrium with a fixed RH. The diagram is simplified because the curve follows a different path depending on whether it is plotted with increasing or decreasing RH. This is known as hysteresis, and hardly matters in practice in the indoor climate.
Absorbed water has to push apart the host molecules to make a place for itself. The dotted line shows the dimensional change in paper caused by water absorption in the material, relative to 20°C and 50% RH. To read this value, choose a particular point on the sorption curve, then trace back horizontally to the strain line, then vertically to the scale at the top of the graph. Dimensional change of cellulosic materials consequent on RH change is larger than dimensional change caused by temperature, within the normal variation of the indoor environment.
An important consequence of the (approximate) temperature independence of water content and equilibrium water content is that hygroscopic materials buffer the RH of their environment when the temperature changes. There is a relatively large quantity of exchangeable water in materials compared with an equal volume of space, so hygroscopic materials are also good at buffering their environment against change of RH caused by air exchange. These matters are explored in more detail elsewhere in this compendium.
The thermal conductivity (λ or k) is the proportionality constant in the Fourier equation, which defines the heat flow through a material as proportional to the temperature gradient across it, in degrees per metre. The unit is usually watts per meter per degree. The watt is a joule per second.
The thermal conductivity is a property of a single material, so it is not immediately useful in calculating heat loss through a wall with various components. For this purpose it is more convenient to consider the temperature difference across the wall, regardless of its thickness and varying composition. The U-value expresses the heat flux per square meter per degree temperature difference across the specimen. The temperature gradient is not explicitly defined, since it may vary through a laminated structure. The unit is watts per square meter per degree.
The resistance to heat flow, the R-value is the reciprocal of the U value. Its usefulness is that it is additive: if you add insulation to an existing wall, just add the individual R values to get the total resistance. Then take the reciprocal to arrive at the U value, which can be used to calculate the heat loss through the building envelope.
The thermal diffusivity is the ratio of the thermal conductivity to the heat capacity. This is an important concept. A material with a high heat capacity will impede transient heat flow, even if it has a high thermal conductivity. Since the natural temperature is not constant, the diffusivity is an important element in designing low energy buildings.
An analogous set of definitions describe moisture diffusion. Indeed, physicists describe water vapour diffusion by simply changing the name of the diffusion law from Fourier to Fick. Chemists will disagree with this as a greatly simplified analogy, but that is how most of the predictive computer programs calculate water vapour diffusion.
Vapour permeability (δ) is the ratio of moisture flux and the magnitude of the vapour pressure gradient. Its unit is kilograms per meter per pascal per second. It is an exact analog of thermal conductivity.
Moisture diffusivity (Dw) is the ratio between the permeability and the moisture capacity. Moisture capacity is the gradient of the sorption curve, for example the tangent to the curve for cellulose, shown above. In the indoor climate it can be taken to be a constant for each material but it increases so much at high RH that this variation must be taken into account when calculating the performance of outer walls. The unit is square meters per second. This also is analogous to thermal diffusivity. Unfortunately, there is a rival definition of moisture diffusivity in the literature.
The published descriptions of moisture movement through porous materials use a variety of definitions, making the literature difficult to follow. A helpful reference is:
M. Kumar Kumaran, International Energy Agency Annex 24 - Heat, air and moisture transfer through new and retrofitted insulated envelope parts (Hamtie). Final report, volume 3, Task 3: Material Properties. Published by Laboratorium Bouwfysica, K.U.-Leuven Belgium. 1996 ISBN 90-75741-01-4.
With a title like this, one would think the book deserves oblivion, but it is actually a useful reference work. Otherwise, wikipedia provides definitions of varying clarity.
Chemical reactions are generally accelerated by increasing temperature and RH. This matter is discussed in the chapter on the Arrhenius concept.
Many articles in the scientific literature demonstrate the preservative effect of cold and dry conditions. For conservators the dilemma is that a cold and dry climate embrittles and stresses materials and constructions formed in warm and humid conditions, often the 100% RH and over 30°C of the animal body or the growing tree, not to mention the 1000° of flowing metal during casting. Mechanical damage can occur within minutes of a climate change, whereas chemical damage seldom shows up so quickly. One can cynically observe that this is why most museum standards demand comfortable (for humans) warmth and a moderate RH - but with added constancy.
Light is included in the list of climatic influences because the energy in light, and in the accompanying infra red radiation, is an important influence on the indoor climate. The discussion below describes the energy in light as a climatic actor, rather than the human reaction to light quality and quantity.
Light is that range of electromagnetic radiation that the human eye detects. The first thing to notice about solar radiation is that about half of its energy is concentrated in the visible range of wavelengths. Most of the rest is in the infra red wavelength range, which provides heat which is sometimes useful but usually is unwanted. Within the visible range, the human eye has a varying sensitivity, detecting yellow-green light better than other colours. We mostly use differences in luminosity of the scene to interpret it, so a light source producing only yellow green light will provide the best conversion efficiency of physical radiant energy into human visual sensation. Low energy bulbs therefore emit most energy at this colour. However, colour is also significant to us, even though the eye is not very sensitive to blue and red light, so even high efficiency lamps add just enough red and blue radiation to fool us into thinking they emit white light comparable with daylight.
The sensitivity of the eye to radiation wavelength is defined through the V-lambda curve.
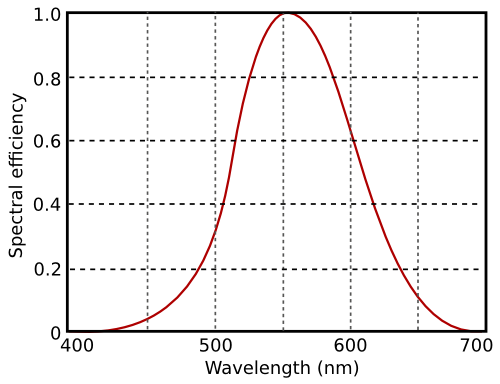
The V-lambda curve describes the relative sensitivity of the eye to different wavelengths of light.
Light sources, even those with the same general description, such as fluorescent lamps, have different spectral energy distributions. The next picture shows at the top a general purpose fluorescent lamp designed for high efficiency. The spectrum below is for a colour matching lamp with enhanced blue and red components. Such a lamp is inherently less efficient in terms of light production for a given power input. The current emphasis on energy efficiency inevitably leads to poor colour rendering.
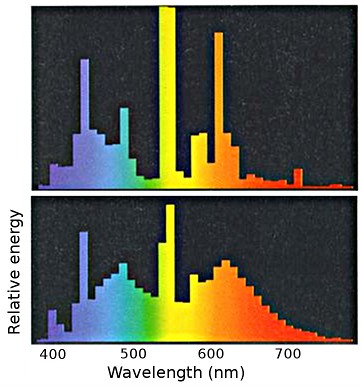
Spectral energy distribution of light from a high efficiency fluorescent lamp (top) and from a colour matching lamp (bottom).
Light is a human response to a physical form of energy. Light intensity is defined by the SI unit of power, the watt, modified by the sensitivity of the human eye as described by the V-lambda curve. However, the fundamental unit, the candela, avoids this complication by being defined at a single wavelength at the top of the V-lambda curve at 555 nm. The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 x 1012 hertz (corresponding to a wavelength of about 555 nm)and that has a radiant intensity in that direction of 1/683 watt per steradian. This is the third successive definition of light intensity, the first being an actual candle and the second a centimetre square of solidifying platinum. The mysterious 1/683 factor is to give the same numeric value as the previous standard. The current definition is much more abstract and unrealistic and difficult to comprehend in an intuitive way. In practice, the output from any lamp emitting energy over a spread of wavelengths has to have its power at each wavelength reduced by the fraction defined by the V-lambda curve. The candela value for a real lamp is the sum of the power in all these wavelength portions.
The candela unit works well for lighthouses on wave-battered rocky headlands (typically 10,000 cd). The light is a point source in a dark scene. The distance at which it can be seen depends on its output in candela: the radiant power in a single direction. In all non-nautical contexts other than firework displays we are more interested in the shape and colour of extended objects illuminated by the light source. For this we need to know the radiant flux emitted into space, followed by the amount falling on a given area of the object we are looking at.
The unit of luminous flux pouring out of a light source is the lumen. This is much simpler to understand - it is the light power emitted into the same steradian cone as was used in the definition of the candela. So a light source emitting one candela uniformly over one steradian produces a light flux of one lumen. You can think of this as invisible light in transit from a point source towards an object that will scatter some of it into your eye. A lamp emitting in all directions with one candela will emit 4π lumens = 12.57 lumens.
Practical light sources, particularly fluorescent tubes, have an extended source area of relatively low luminosity, radiating light in a non-uniform pattern. By some magic calculation, manufacturers integrate the candela values in all directions into the lumen emission from the lamp. This is then divided by the power supplied in watts to give the lumen per watt which is the favoured unit of green sages. However, it is not the whole story about lighting efficiency, because the light has to be directed efficiently. For exhibitions, this usually means spotlighting the object while providing a darker, but not black, background lighting to provide a good sensory experience. Tungsten quartz halogen incandescent lamps are still the favourite light source of exhibition designers. They will soon be forbidden, so the natural successor is light emitting diodes, which also give a well focussed light beam. The lumen per watt from the Q-halogen lamp is about 24 lm/W. Light emitting diodes are in rapid development but presently (2009) give better than 100 lm/W. For comparison, total solar radiation gives 93 lm/W but with infra red filtered out the efficiency increases to 250 lm/W, making daylight through infra-red reflecting glass the most energy efficient, but also the most unruly light source. The maximum theoretically possible efficiency from a monochromatic source at 555 nm, is 683 lm/W. The necessary compromise between luminous efficiency and full spectral radiation to give adequate colour rendering is a complicated discussion which is not considered in this article.
The last unit of light requiring definition is the amount of light impacting an object, to make it visible by scattering and reflection and to cause decay, in some materials, by provoking photochemical reaction. The lux is the flux of light from one candela uniformly distributed over the above mentioned steradian cone, at a distance of 1 metre from the source.
Note that the lux value gives no information about the spectral energy distribution of the light, so the photochemical potency is undefined. It varies by a factor of 20 between daylight and tungsten incandescent light, because short wave radiation is very photochemically active but also very weakly emitted from a tungsten lamp. Furthermore the visibility of the illuminated object depends on its ability to reflect, scatter and absorb the incident light. So the lux value is not terribly useful, but is universally used by conservators as the vital measure of light intensity for ensuring good preservation.
Tim Padfield, September 2009

This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 License.