|
|
Stress, strain and craquelure - 4 |
A painting on canvas hanging on a wall is not apparently exposed to any significant changes in strain. Its dimensions are fixed by a strong wooden frame which does not expand or contract much with changing temperature or RH. So what use can we make of a set of diagrams which relate movement to applied stress?
If I tug at both ends of a strip of oil paint the stress is transmitted right along the strip so that at any point there is an internal stress that is exactly the same magnitude as that which I apply across the ends.
Now suppose that I clamp the two ends firmly, under slight stress, as if the strip were stretched across the frame of a painting. I then put the assembly in a desiccator. The paint will try to shrink as it loses water but the shrinkage is restrained and therefore invisible. There is, however, a considerable internal stress developed, maybe enough to threaten cracking of the paint. How can we estimate it?
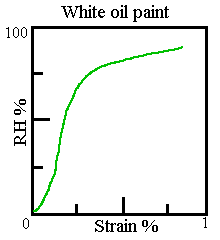The stress can be estimated from the RH-strain diagram for paint which is hanging freely. The RH-strain diagram for white lead oil paint looks like this, with apologies to Marion Mecklenburg for a sketch version of his precise original diagram.
Suppose that the RH goes down from 50% to near zero. The paint will try to shrink by about 0.2% but cannot. What now is the stress? We find it, approximately, by transfering this value, 0.2%, to the mechanical stress strain diagram shown earlier (for yellow paint, but never mind the colour just feel the strain) and find that such a 0.2% strain corresponds to 0.25 MPa stress. This must be the extra stress within the paint film caused by the loss of water.
Another way of looking at the matter is to imagine the process happening in two steps: first allow the paint strip to shrink unrestrained as it loses water and then pull it back to the original size, measuring the resulting mechanical stress.
I should use a mechanical stress-strain diagram measured at low RH to obtain the correct stress in the dried strip. In fact I used Mecklenburg's values for 50%RH. You will now begin to understand how much diligent research is needed just to amass the starting data for sensible deductions about why paintings react as they do to environmental change.
If the stress generated by the RH change, (or by temperature change, which is just as potent a cause of trouble), exceeds the breaking stress of the paint layer, it will crack. The cracks will, however, be in a quite different direction to those caused by expanding the frame (keying out in conservator jargon) as explained in part 2.
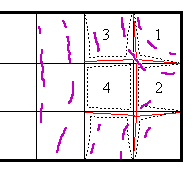
Consider the right hand end of a rectangular painting which has just been cooled by 20 degrees. The paint is trying to shrink but is restrained by the stiff frame. Although the outer dimensions remain fixed there is some invisibly slight rearrangement of the paint in the interior of the picture.
The thin continuous lines represent the original position of squares of paint. When the RH is reduced each square will try to shrink uniformly. Square number 1 is, however, restrained on two sides where it is fastened to the frame. It will tend to distort as it shrinks, as shown by the dotted line. Squares 2 and 3 are restrained on one side, so they distort less. Only square 4 can move all four of its sides. It is tugged by the shrinking square to its left but also very strongly by the corner squares which can only move their corners which are adjacent to square 4. The result for square 4 is a slight distortion (strain) towards the two corners of the frame.
If the paint is sufficiently brittle it will crack in directions that release the strain, that is across the direction of the stress, as shown by the purple lines. The curvature of the cracks into the sides is caused by the highest stress becoming parallel to the line where the edges of the squares are restrained by the frame.
In the middle of the picture the cracks tend to run parallel to the short sides. They spread from the middle towards the stressed locked edges, while the cracks starting at the short sides curl round as shown in the diagram.
This is a visual, intuitive version of the finite element analysis pioneered, in the field of painting conservation, by Marion Mecklenburg. His numerical analysis of the effect of temperature change suggests that cooling stresses are fairly uniform over a canvas, increasing by only about 5% at the corners. This means that if a painting is going to crack through cooling stresses it will crack all over.
Marion's analysis of drying stresses, however, shows a dramatic increase of stress into the corners. This stress, directed diagonally towards the centre of the picture, is over double that in the centre of the picture.
So far, the effect of the canvas has not been mentioned at all. That comes in the next section.
This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 License.