
 |
What happens to water absorbent materials below zero degrees? |
Relative humidity (RH) below zero is defined as the actual water vapour pressure in the air (or space) divided by the saturation vapour pressure over ice. Water absorbent materials, however, tend to maintain an equilibrium with supercooled water as their temperature is reduced below zero celsius. This has the curious consequence that it is possible to dry out absorbent materials in a sub-zero atmosphere at 100% RH.
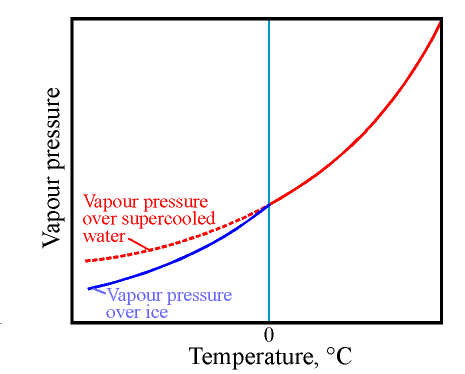
The first diagram shows water vapour concentration (by a peculiar convention quoted in units of pressure) over water, the solid red line. This is extended below zero degrees as a dotted line representing the vapour pressure over supercooled water, which can exist for a long time just a few degrees below zero. The blue line is the vapour pressure over ice. The diagram is distorted to exaggerate the divergence of the line for ice.
In the next diagram I add lines which represent the vapour pressure over materials which contain water but are not saturated. It is a general rule, stated elsewhere in this series of articles, that absorbent materials have, at a constant water content, a vapour pressure which follows quite closely the curve for a constant RH as the temperature changes.
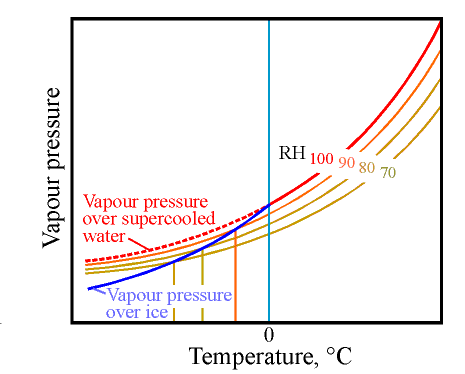
All I need to do therefore is to draw in the familiar (!) fan pattern of RH lines of the psychrometric chart. Just the high RH curves are shown in this diagram.
The curve marked 70% RH, for example, is close to the actual curve for vapour pressure over wood with 15% water content. Notice that I have drawn smooth curves for 90, 80 and 70% RH without a kink at the zero of temperature. They pass smoothly through zero, maintaining their proportionality to the curve for vapour pressure over supercooled water.
There is no reason why there should be a kink in the curve for vapour pressure over wood. The water molecules are probably weakly bonded to the hydrophilic groups of the cellulose molecules and in a form quite unlike the structure of water, or of ice. The sudden stability of the highly ordered ice structure below zero has no significance in the molecular environment of the cell walls of a piece of wood. Only when the temperature has dropped to the point where the curve for the vapour pressure over ice crosses this vapour pressure curve for wood can ice coexist with the wood. At this point ice will begin to form within the voids of the wood, drawing water molecules out from their absorption sites in the cell walls. The wood substance will therefore dehydrate, at 100% RH. The water released will condense as ice on the surface or in voids in the structure.
I have used wood as an example but the argument also applies to the only archive material where storage below zero celsius is strongly recommended: colour film. If the film is first equilibrated to about 40% RH at room temperature its vapour pressure curve will first cross the curve for vapour pressure over ice at some point below minus fifty degrees. Above this temperature there is no danger of ice forming in voids between sheets of film.
This argument applies to a system which is at a uniform temperature. As soon as there is a temperature difference the matter becomes more complicated, so the process of taking film out of a very cold place to look at it is not trivial. I will return to this matter in a later article.
The argument sketched above for wood can be developed more stringently, or at least more convincingly, by considering the behaviour of a salt solution.
In the welfare state called Denmark the local authority uses a part of my tax contribution to strew salt liberally over the cycle paths to reduce the chance of me cracking my head on the ice in winter. This humane use of masses of salt is a very recent development and will certainly keep building conservators in work for years to come as the salt creeps into the foundations, up the walls and then pushes the plaster off the walls. You would think we would have learned from Venice. But let us look at the physics of the beneficial effects of salt, reserving the story of its brutal attack on our historic buildings to a later article.
A saturated solution of sodium chloride is, at room temperature, in equilibrium with 76% RH in the space above it, almost unaffected by temperature. This phenomenon can be explained like this: the sodium and chloride ions are not volatile and so stay in the liquid but water molecules are free to explore the space above the liquid. Their tendency to escape into space is impeded by the salt ions at the surface of the solution, and by the weak electrostatic forces that bond water molecules to the charged ions. These effects reduce the rate of escape compared to that from pure water. The water molecules in the space above the liquid are not affected in any way by the saltiness of the water below and their return to the liquid is not more difficult than if they were returning to pure water. An equilibrium is established in which the water vapour concentration above the solution is lower than that over pure water. In the case of a saturated salt solution this concentration is about three quarters of that over pure water: the RH over the salt solution is 76%.
If this solution is cooled to 5 degrees below zero it will not freeze. This is because the water vapour pressure over the solution is below that over ice, as shown in the diagram by the vertical separation of the interpolated 75% RH contour below the curve for the saturation vapour pressure over ice.
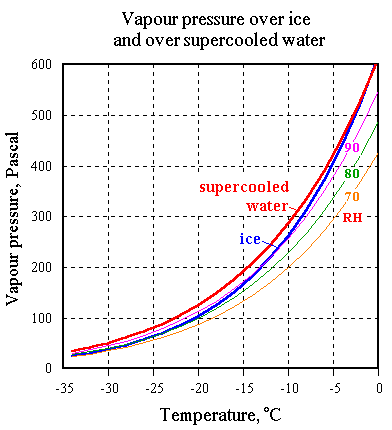
This diagram is similar to the sub-zero portion of the diagram in the previous section, but is drawn accurately.
If one drops a lump of ice into the saturated salt solution at this temperature the ice will disappear. One can explain this in a formal way by saying that water will evaporate from the ice and find itself at too high a vapour pressure to be in equilibrium with the nearby surface of the salt solution and will therefore recondense into the solution. This process will continue, if there is enough ice, until the salt solution has diluted itself until it is in equilibrium with about 96% RH, at which point the vapour pressure over the solution is the same as that over ice. In reality, the transfer of water from ice to solution occurs mostly at the interface between these two phases, rather than through the air, but the equilibrium is easiest explained by regarding the air above the mixture as a transit lounge for flying water molecules.
Depending on the temperature therefore, even a rather dilute salt solution will dissolve ice.
A saturated salt solution and pure ice have the same vapour pressure above them at about minus 21 degrees, so below that temperature it is unwise to cycle.
When waterlogged materials are put into a freezer the situation is different because there is now nearly pure water in the spaces within the material. This water will readily form ice as soon as the temperature drops below freezing. Within the paper fibres of a water saturated library book rescued from a flood for example, there is still bound water that does not freeze and it will exert a vapour pressure lower than that over supercooled water but greater than that over ice. At -5C, for example, the paper fibres will tend to dry to equilibrium at about 96% RH, with respect to supercooled water. The lost water will accumulate as ice crystals separate from the fibres. The paper is beginning to dry even though the RH in the freezer, as measured against ice, is 100%. As the temperature is further reduced, more water will come out of the fibres and condense onto the ice crystals that fill the larger spaces between the fibres. This ice will grow and expand, pushing apart the drying fibres.
This phenomenon is a particular problem in freeze drying wood. When the wood is cooled below freezing, ice forms in the cell lumen, the empty space within the cell. More water comes out from the cell wall, which therefore shrinks at the same time as the ice lens in the lumen is expanding. This is definitely an undesirable situation. The process can be stopped, in theory, by impregnating the cell wall with a substance that further reduces the vapour pressure over the cellulose-water complex so that it does not lose water. Salt should do this. Suppose that the wood is first impregnated with a weak salt solution, so that ice begins to form in the lumen at about -5°C. Freezing out of pure water will cause the salt solution to concentrate so that the ions diffuse into the still unfrozen region within the cell wall. This will further reduce the vapour pressure in equilibrium with the cell wall so that it is always equal to that of ice. There is now no loss of water from the cell wall until the ice has been vapourised away in the freeze drying process. Dehydration of the cell wall is prevented, as long as the temperature is above about -22C. There are several other materials that perform the same function and are preferred for other reasons. Polyethylene glycol and sugar are two water soluble materials that have been used to prevent the untimely dehydration of wood before the ice has been removed from the lumen.
The physics of water in materials below freezing is not easy to understand. I thank many colleagues for helpful discussions and particularly Poul Jensen, Chief of the section for conservation of waterlogged wood in the National Museum, who suggested the topic.

This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 License.